At first, we sample ![]() in the
in the ![]() (
(![]() is odd) equidistant points around
is odd) equidistant points around ![]() :
:
![]()
Then we interpolate points
(1) 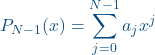
(2) ![]()
Here is reference to non-existing equation (??).
–
At first, we sample ![]() in the
in the ![]() (
(![]() is odd) equidistant points around
is odd) equidistant points around ![]() :
:
![]()
(1) 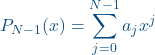
(2) ![]()